Option Greeks

Option Greeks are essential tools in quantitative research, particularly in options trading and risk management. They measure the sensitivity of an option's price to various factors, which are crucial in building and testing trading strategies. Below is an overview of how they are used, derived, and their properties:

Areas where Option Geeks are predominantly used

• Risk Management - Risk Managers make use of Option Geeks to quantify different risk associated with options trading like Delta hedging uses the Delta Greek to neutralize the impact of price changes in the underlying asset.
  Volatility Analysis: Vega is extensively used in analyzing the impact of volatility on option prices. Quants use this to identify potential mispricings in options and arbitrage opportunities.

• Optimization: Greeks are used in optimization algorithms for portfolio construction, ensuring the portfolio is optimized for risk-adjusted returns.

Types of Option Geeks

Delta (𝚫) - Delta Measures sensitivity of change in price of option with change in price of underlying 𝚫 = 𝝳v / 𝝳s where v is the option price and s is price of underlying asset. Delta ranges from 0 to 1 for call options and it ranges from -1 to 0 for Put options. A Delta of 0.5 means that if the underlying asset’s price increases by $1, the call option’s price is expected to increase by $0.50. Delta of 1 means the option's price moves one-for-one with the underlying asset.

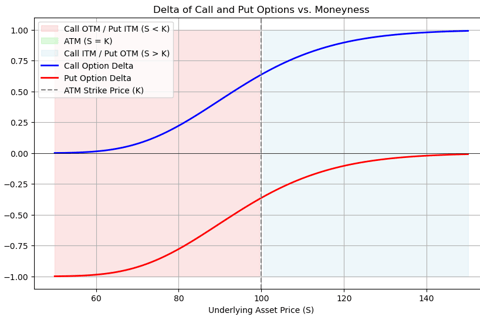
• Moneyness of Option Vs Delta:

  • At-the-Money (ATM): Delta is approximately 0.5 for a call option and -0.5 for a put option when they are at-the-money.

  • In-the-Money (ITM): Delta approaches 1 for deep in-the-money call options and -1 for deep in-the-money put options.

  • Out-of-the-Money (OTM): Delta approaches 0 for out-of-the-money options, whether they are calls or puts.

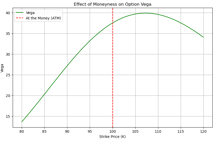
Following graphs Illustrate above phenomenon. As can be observed from the graphs as option becomes more in the money delta inches closer to 1 for call and -1 for put and as option price starts becoming out of money delta approaches to 0.

Derivation of Delta

Delta is derived from the pricing models used to value options, such as the Black-Scholes model. For a European call option, the Delta can be calculated using the Black-Scholes formula Δcall​=N(d1​),

where,

• N(d1) is is the cumulative distribution function of the standard normal distribution

• S is the current price of the underlying asset.

• K is the strike price of the option.

• r is the risk-free interest rate.

• σ is the volatility of the underlying asset.

• T is the time to expiration (in years).

For a European put option, the Delta can be calculated as Δput=N(d1)−1

Applications of Delta

• Delta Neutral Hedging Strategy - Delta is crucial for hedging purposes. To hedge a long option position, a trader might short the underlying asset in proportion to the option's Delta. This is called "Delta Hedging." Example: If a trader holds a long call with a Delta of 0.6, they might short 60 shares of the underlying asset to hedge against price changes.

• Delta-Neutral Strategies: A strategy is Delta-neutral when the sum of all Deltas in the portfolio is zero, meaning the portfolio is insensitive to small changes in the underlying asset's price. Traders continuously adjust their positions to maintain Delta neutrality, especially in market-making.

Gamma (Γ): Gamma is second order Geek which measures sensitivity of delta to change in price of underlying. Higher the Gamma higher is the risk in delta trading strategies.

where:

• V is the price of the option.

• S is the price of the underlying asset.

• Δ is the Delta of the option.

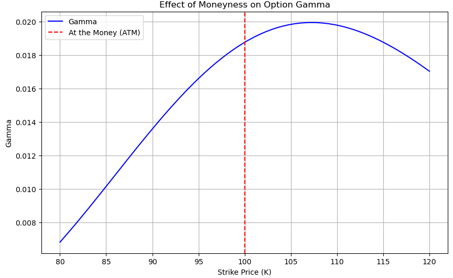
• Moneyness of Option Vs Gamma:

  • At-the-Money (ATM): Gamma reaches its maximum value when the option is at-the-money (ATM), meaning the underlying asset price is approximately equal to the strike price (S ≈ K). This is because small movements in the underlying asset price will have the most significant impact on Delta when the option is ATM. When an option is ITM or OTM, small changes in the underlying have a less significant effect on Delta.

  • In-the-Money (ITM) and Out-of-the-Money (OTM): : Both in the money and out of money options have lower value of Gamma as price around these points move one to one with price of underlying showcasing less sensitivity to change in price of underlying

Derivation of Gamma

Gamma depends on Underlying asset price, volatility and time to maturity

Above formula derives value of Gamma based on Black-Scholes model where N'(d1) is the probability density function of standard normal distribution S0 is price of underlying and T is time to Maturity

Applications of Gamma

• Vega Gamma Trade off - Options with high Gamma are often more sensitive to volatility changes (Vega). Traders use Gamma to balance these sensitivities and understand the trade-offs between Delta hedging and volatility risk.

• Managing Delta Risk: A higher Gamma indicates that Delta will change more rapidly, requiring more frequent adjustments to maintain a Delta-neutral position. Knowing the Gamma of a portfolio helps in planning and executing these adjustments to minimize risk.

Vega (Ṽ) - is one of the key Greeks in options trading, measuring the sensitivity of an option's price to changes in the volatility of the underlying asset. Unlike Delta, Gamma, and Theta, which are influenced by the underlying asset's price or time decay, Vega specifically captures the impact of volatility on an option's value. Vega quantifies how much the price of an option is expected to change with a 1% change in the implied volatility of the underlying asset.

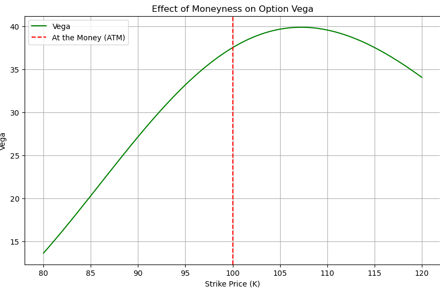
Characteristics of Vega:

• Positive for Both Calls and Puts: Vega is always positive for both call and put options. This means that an increase in volatility generally increases the price of both types of options.

• Highest at ATM: Vega is highest for at-the-money (ATM) options. This is because ATM options are more sensitive to changes in volatility compared to in-the-money (ITM) or out-of-the-money (OTM) options.

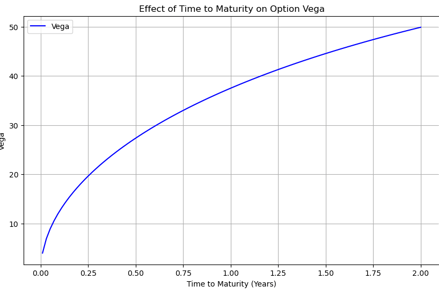
• Decreases with Time to Maturity: As the option approaches its expiration date, Vega decreases. Options with longer time to maturity have higher Vega because there is more time for the underlying asset's price to fluctuate.

Derivation of Vega Using Black- Scholes Model - For a European call or put option, Vega is given by

where,

• S0 = Current price of the underlying asset

• T = Time to maturity

• N′(d1) = Probability density function of the standard normal distribution evaluated at d1

Applications of Vega

• Volatility Strategies: Traders use Vega to construct strategies that profit from changes in implied volatility, such as straddles, strangles, and iron condors. High Vega implies a higher premium for options due to increased uncertainty in the underlying asset's future movements.

• Vega Neutral Strategies: Some traders aim to create Vega-neutral portfolios, where the overall Vega is zero. This minimizes the portfolio's sensitivity to changes in volatility, focusing instead on other factors like Delta and Theta.

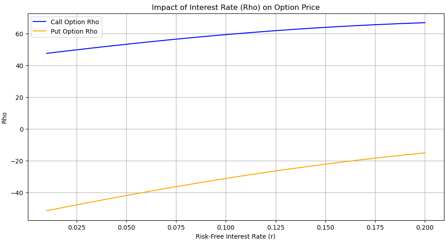
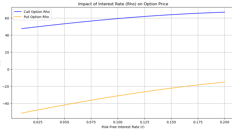
Rho(Ŕ) Rho represents the rate of change of the option's price with respect to a change in the risk-free interest rate. For call options, Rho is generally positive, meaning that an increase in the risk-free rate will increase the call option's price. For put options, Rho is typically negative, indicating that an increase in interest rates will decrease the put option's price.

Derivation of Rho - Using Black-Scholes model Rho for call option is derived as follows

Where:

• K = Strike price

• T = Time to maturity

• r = Risk-free interest rate

• N(d2) = Cumulative distribution function of the standard normal distribution

Characteristics of Rho:

• Impact on Long-Term Options: Rho has a more significant effect on options with longer maturities. This is because the present value of the strike price is more sensitive to interest rate changes over a longer period.

• Relatively Low Impact on Short-Term Options: For options with a short time to maturity, Rho's impact is minimal since the change in the present value of the strike price is less significant.

• Higher for Deep In-the-Money Options: Rho is higher for deep in-the-money call options and lower for deep in-the-money put options because these options are more influenced by the cost of carrying the underlying asset over time.

• Impact of Rho based on Interest Rates - An increase in interest rates raises the opportunity cost of holding cash. Since buying a call option allows an investor to gain exposure to the underlying asset without immediately paying the full price, higher interest rates make this deferred payment more attractive, increasing the option's value. And opposite is the case for Put option With higher interest rates, the cost of carrying the underlying asset increases, making it less advantageous to hold the right to sell the asset. Additionally, the opportunity cost of holding a position that benefits from price declines becomes higher, reducing the attractiveness of the put option.

Application of Rho in Options Trading:

1. Interest Rate Changes:

   • Impact on Option Prices: Rho helps traders understand how changes in interest rates will affect option prices. When interest rates rise, call options become more valuable, and put options become less valuable, as the cost of carrying the underlying asset increases.

   • Hedging Interest Rate Risk: Traders with large options portfolios may use Rho to hedge against interest rate risk, especially if they have positions with longer maturities.