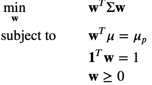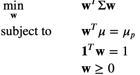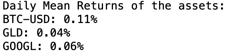Portfolio Allocation and Diversification

Its rightly said that we should never place all our eggs in same basket, Portfolio diversification plays key role in minimizing market risks associated with assets. Most commonly used portfolio optimization techniques include. Mean Variance Optimization , Capital asset pricing Model

Mean Variance Optimization

Mean variance Optimization technique aims at identifying asset allocation weights which minimizes portfolio variance for expected mean returns of the Portfolio. Mean variance optimization technique was formulated by Markowitz. Mean Variance Optimization technique is constrained optimization problem. Some common constraints include Budget constraints, Target return constraints, Non Negativity constraints, Transaction cost and other liquidity constraints. Following optimization equation explains the construct of Mean Variance optimization. where w is the weight of assets in our portfolio 𝞵 is the expected returns of assets in portfolio with following constraints of expected return of portfolio = 𝞵p and sum of weights of assets in portfolio = 1

Following steps entails High level working of Mean Variance Optimization

• Estimate Expected Returns and Covariances:

  • Expected Return (E[Ri]): The mean return of asset i.

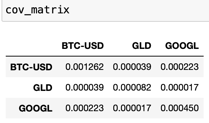
  • Covariance Matrix (Σ): A matrix capturing the covariance between each pair of assets.

• Formulate the Optimization Problem:

  • Objective Function: Typically to minimize the portfolio variance 𝞼p^2 ​ subject to a constraint on the expected return.

  • Constraints: The sum of the weights of all assets equals 1 and The portfolio return should meet or exceed a target return 𝞵p

• Solve the Optimization Problem: This is usually achieved using quadratic programming.

Lets work this out with an example -

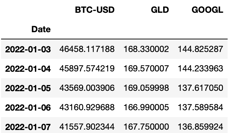
Step 1: Creating Dataframe for 3 asset classes (Google Stock , Gold, Bitcoin)

Step 2: Calculating expected daily return and covariance for above assets

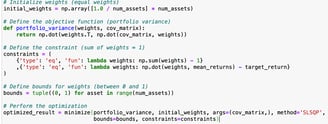
Step 3 : Defining target return of the portfolio (0.08% in our case)

Step 4 : Initializing equal weights of all the assets in the portfolio and setting up the optimization function to minimize portfolio variance with above defined constraints

Considering closing price data of following assets Google Stock, Bitcoin and Gold for period Jan 2022 to June 2024. Mean Daily Returns of the above assets are as follows Google 0.06% , Bitcoin 0.11% and gold 0.04%. Our goal here is to create a portfolio with Targeted Mean Daily return of 0.08% while keeping the volatility as low as possible. Based on above data and our Target return of 0.08% Mean Variance Optimization technique resulted in following weights for each asset class Bitcoin - 52% , Gold 20% and Google stock 28% with volatility of 2.1%. Note I made use of SLSQP (Sequential Least Squares Programming) algorithm involves the linearization and quadratic approximation of the objective function and constraints.

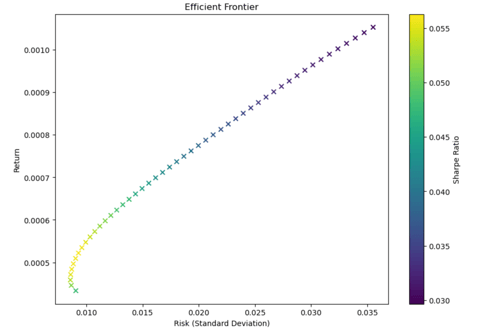
We can also choose target return based on given level of risk using efficient frontier. The efficient frontier is a key concept in portfolio theory that represents the set of optimal portfolios offering the highest expected return for a given level of risk (standard deviation), or equivalently, the lowest risk for a given level of expected return. Below diagram represents the efficient frontier for all the above assets that we have considered. Risk- Reward relationship of higher the risk higher is the reward can be clearly observed from the efficient frontier. As risk increases, the additional expected return gained from taking on more risk may not be sufficient to compensate for the increased risk. This results in a lower Sharpe ratio. This is also very evident from the efficient frontier